齐次坐标的理解

在学习矩阵变换时学到了齐次坐标，觉得很有意思，就深入研究了一下这个概念。

我的老师对我说，学习最有效的办法就是将学到的知识重新讲出来，这样自己会记得更牢，也会有更深刻的认识。

以下是我的个人理解，我是第一次学习齐次坐标这个概念，在编写过程中难免会出现错误，遗漏，也欢迎各位大佬前来指出我文章中的不足，我会虚心改进。

齐次坐标是什么

齐次坐标就是在原有的笛卡尔坐标上加上一个维度（升维），用来在投影空间计算几何图形。

比如一个二维的点P(x, y)，转换成齐次坐标后就是P(x, y, w)。

齐次坐标的优点

1.表示无穷远点

投影空间和欧氏几何空间最大的特点就是：在欧式几何空间中两条互相平行的直线，在投影空间中会"相交"，怎么样，是不是有点反直觉了，明明小学时老师就说过了：“两条相互平行的直线永远不会相交”的道理了，不如来看一张图：

railway

这是一个铁轨，可以看到两条互相平行的铁轨，在无限远的地方会相交于一点，但是我们都知道，实际生活中，这两条铁轨并不会相交到一起，这是因为我们所在的世界是在一个欧氏几何空间，而我们眼睛所看到的图像是一个投影空间（3维物体在2维平面上的投影）。

两条轨道交点在无限远的位置，如果是在笛卡尔坐标系中，只能用(∞, ∞)来表示，如果在齐次坐标系中，则可以用(1, 2, 0)来表示，因为数学运算中不能除以0，所以使用0来表示无限（Infinity）

个人注解：这里我理解的也不是很透彻，只是0不能做被除数（没有定义计算结果），所有就有了这么个定义：除以0表示无限大小，这只是个定义：(1/0, 2/0)≈(∞, ∞)，具体为什么要这样定义，我还在研究中

2.用乘法表示平移变换

使用乘法运算来进行平移变换可以使计算过程更加简洁，结构更加清晰。

有一个点P(x, y)，现在我们对点P进行变换，变换后的结果用P'表示

首先是旋转变换，旋转角度使用θ(theta)表示：

\begin{bmatrix} P'_x \\ P'_y \end{bmatrix} = \begin{bmatrix} cos \theta & -sin \theta \\ sin \theta & cos \theta \end{bmatrix} \begin{bmatrix} P_x \\ P_y \end{bmatrix}

然后是缩放变换，缩放向量使用S表示：

\begin{bmatrix} P'_x \\ P'_y \end{bmatrix} = \begin{bmatrix} S_x & 0 \\ 0 & S_y \end{bmatrix} \begin{bmatrix} P_x \\ P_y \end{bmatrix}

最后是平移变换，平移向量使用t表示：

\begin{bmatrix} P'_x \\ P'_y \end{bmatrix} = \begin{bmatrix} P_x \\ P_y \end{bmatrix} + \begin{bmatrix} t_x \\ t_y \end{bmatrix}

上面的变换操作均是在笛卡尔坐标空间中进行的，可以看到旋转变换和缩放变换是乘法运算，但是平移变换却是加法运算，如果涉及非常多的变换，整个公式会变得非常复杂。

如果引入齐次坐标，就可以将平移变换由加法转换为乘法，将缩放、旋转、平移操作统一起来，表示一连串的矩阵相乘的形式，计算起来非常方便。

齐次坐标表示旋转变换：

\begin{bmatrix} P'_x \\ P'_y \\ 1 \end{bmatrix} = \begin{bmatrix} cos \theta & -sin \theta & 0 \\ sin \theta & cos \theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} P_x \\ P_y \\ 1 \end{bmatrix}

齐次坐标表示平移变换：

\begin{bmatrix} P'_x \\ P'_y \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & T_x \\ 0 & 1 & T_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} P_x \\ P_y \\ 1 \end{bmatrix}

齐次坐标表示缩放变换：

\begin{bmatrix} P'_x \\ P'_y \\ 1 \end{bmatrix} = \begin{bmatrix} S_x & 0 & 0 \\ 0 & S_y & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} P_x \\ P_y \\ 1 \end{bmatrix}

3.区分点和向量

平移T、旋转R、缩放S是三个最常见的仿射变换。

平移变换只对点(Point)有意义，而向量(Vector)只有方向和大小的概念，并没有位置的概念，而旋转、缩放对向量和点都有意义，如果现在只有三个分量A(1, 4, 5)，就无法区分这是个向量还是点了。

	对向量来说	对点来说
平移变换	没有意义	有意义
旋转变换	有意义	有意义
缩放变换	有意义	有意义

齐次坐标中，使用w分量来区分点和向量，如果w=0，则表示一个向量，如果w!=0，则表示的一个点

根据齐次坐标与笛卡尔坐标的转换规则，将A(x, y, w)转换成笛卡尔坐标，如果w分量等于0的话，除法表达式失去意义，此时A(x, y, 0)表示的就是一个无穷远点A(∞, ∞)，虽然长度无法计算，但是此时A仍然是有方向的，所以A就表示一个向量（齐次坐标中向量只有方向属性，向量长度不重要）

如果w不等于0，结果就是一个点：P(x/w, y/w)

一个标准的空间直角坐标系的基向量是a = (1,0,0),b=(0,1,0),c=(0,0,1)，原点位置为O

用基向量来表示笛卡尔坐标系中的向量就是：（因为向量没有位置的概念，所以没有O（即O=(0, 0, 0)））

V=V_xa+V_yb+V_zc

用基向量来表示笛卡尔坐标系中的点就是：（可以把P点的位置看成是对基点O所进行的一个位移，这个位移向量就是P-O）

P=P_xa+P_yb+P_zc+O

可以看到表达点比表达向量需要一个额外的信息，把上面的公式以矩阵形式表达的话就像这样：

[a, b, c, o]可以看做是基矩阵

V= \begin{bmatrix} a & b & c & O \end{bmatrix} \begin{bmatrix} V_x \\ V_y \\ V_z \\ 0 \end{bmatrix} = \begin{bmatrix} a_x & b_x & c_x & O_x \\ a_y & b_y & c_y & O_y \\ a_z & b_z & c_z & O_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} V_x \\ V_y \\ V_z \\ 0 \end{bmatrix}

P= \begin{bmatrix} a & b & c & O \end{bmatrix} \begin{bmatrix} P_x \\ P_y \\ P_z \\ 1 \end{bmatrix} = \begin{bmatrix} a_x & b_x & c_x & O_x \\ a_y & b_y & c_y & O_y \\ a_z & b_z & c_z & O_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} P_x \\ P_y \\ P_z \\ 1 \end{bmatrix}

仿射变换简单来说就是：线性变换 + 平移变换。而线性变换包括：旋转变换、缩放变换

齐次坐标与笛卡尔坐标的转换

齐次坐标与笛卡尔坐标的转换非常容易，只需要将每个分量都分别除以w分量然后去掉w分量，即可将这个点还原成笛卡尔坐标。

转换公式：

(x, y, w) \quad => \quad (\frac{x}{w}, \frac{y}{w})

从笛卡尔坐标到齐次坐标的转换：

如果(x, y, z)是个点，则变成(x, y, z, 1)

如果(x, y, z)是个向量，则变成(x, y, z, 0)

从齐次坐标到笛卡尔坐标的转换：

齐次坐标P(x, y, z)转换成笛卡尔坐标的话，将每个分量都分别除以w分量，就转换成了一个笛卡尔坐标P(x/w, y/w)

如果是(x, y, z, 1)，则这是一个点，变成(x, y, z)

如果是(x, y, z, 0)，则这是一个向量，仍然变成(x, y, z)

根据转换公式，可以发现一个规律：

Homogeneous \quad \quad Cartesian \\ (1, 2, 1) <=> (\frac{1}{1}, \frac{2}{1}) \\ (2, 4, 2) <=> (\frac{2}{4}, \frac{4}{4})=(\frac{1}{1}, \frac{2}{1}) \\ (3, 6, 3) <=> (\frac{3}{3}, \frac{6}{3})=(\frac{1}{1}, \frac{2}{1})

点(1, 2, 1)、(2, 4, 2)、(3, 6, 3)均对应笛卡尔坐标中的同一个点(1, 2)，用图来解释的话就像这样：

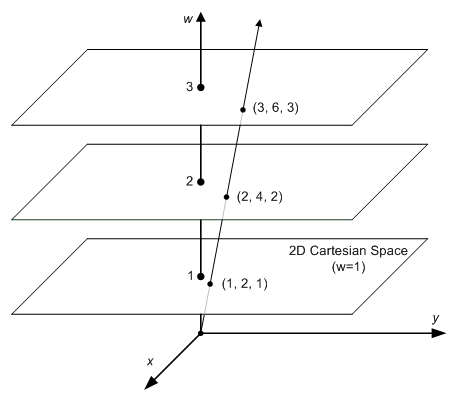
w-field

根据这张图的作者解释，齐次坐标中的w分量就像投影机和幕布的距离一样，当w增加时，投影出的画面和投影机之间的距离也会不断增加。

以下为个人理解：

所谓的w分量，就像是给原先的二维图形升到了三维，在欧氏几何空间中，只要2d图形的x, y分量不变，那么投影图形的x, y也不会改变，即使z轴增加或者减小，最终的投影图形和原图形也是完全一样的，在投影空间里也是同理（只不过投影空间里两条相互平行的直线在欧氏几何空间里不是平行的，就像上图中的两条直线一样）。

笛卡尔坐标就像相机中的正交视图的概念一样，远处的物体和近处的物体一般大。笛卡尔坐标表示的是一个普通的平面直角坐标系（欧氏几何空间）。

齐次坐标更像是相机中的透视视图的概念一样，有近大远小的特点。齐次坐标表示是一个投影空间。

证明两条平行线可以相交

在笛卡尔坐标系中，有两条直线：

\begin{cases} Ax+By+C=0 \\ Ax+By+D=0 \end{cases}

如果C=D，那么这两条直线就是同一条线，如果C!=D，那么此方程无解（不会有交点）

如果放在投影空间里求解（C!=D时）：

\begin{cases} A\frac{x}{w}+B\frac{y}{w}+C=0 \\ A\frac{x}{w}+B\frac{y}{w}+D=0 \end{cases} => \begin{cases} Ax+By+Cw=0 \\ Ax+By+Dw=0 \end{cases} => (C-D)w=0

因为C!=D，所以w一定为0，w为0时该齐次坐标表示的是一个无穷远点，所以两条直线的交点在无穷远的地方。

为什么w=0时表示的是一个无穷远点呢？再来看张图。

railway2

两条铁轨在欧氏几何空间中相互平行，我们随机取一个xz截面，将其定义为w=1，可以看到w越接近0时，L与R之间的距离就越近。即使投影空间中，两条铁轨也并没有真的相交，而是像中学时的反比例函数y=1/x一样，x越大，y就越接近0，但y永远大于0。这里的LR之间的距离同理，随着w的减小而不断缩小，但由于LR之间的距离不会小于等于0，那么w=0也就是在无穷远的地方了。

用图来演示的话，像这样，两条线无限接近，但永远也不会相交，也可以理解为交点在无限远的地方。就像一个数x不断地除以2，其值会越来越小，但永远比0大，w分量在这里同理。

结尾

经过不断地查阅资料后，我渐渐明白了齐次坐标是什么，用在哪，以及如何转换，说实话这花了我不少时间，对我来说，各种概念理解起来很困难，期间学习起来非常不容易，前前后后花了差不多快一个星期才弄懂这些概念，而且有些东西很抽象，没法直观地用图像去描述，学起来是困难重重。

渐渐我发现了一个规律，不管是学什么，刚开始学时总会经历一个两个瓶颈期，如果坚持过去，后面就会很轻松了。被难点卡主时不要放弃，可以试着休息一下，调整好心情后再重新来过，当困难被解决掉时，你会发现之前做的一切都是值得的。